TITULO: Arranca en verde - Tráfico prohíbe la circulación de camiones por la A-7 ,.
El Sabado - 16 , 23 , 30 - Noviembre a las 8:55 por La 1, fotos,.
La actriz y youtuber Leonor Lavado se pone al frente del concurso divulgativo sobre seguridad vial que recorre distintas ciudades españolas a bordo del coche del programa. El espacio fomenta el conocimiento de las normas viales, el civismo y la sostenibilidad ambiental,.
Tráfico prohíbe la circulación de camiones por la A-7,.
La DGT ha decidido levantar parcialmente las restricciones a la circulación en la AP7 y en la A7 en la conexión con la A3, en horario nocturno a los camiones de más de 7,5 Tn. que tenían prohibido circular por esta confluencia debido a los fuertes daños causados por la DAN el pasado 29 de octubre.
La DGT ha decidido levantar ya parcialmente las restricciones a la circulación de camiones en la AP7 y A7 en la conexión con la A3 (kilómetro 336,850) para camiones de más de 7,5 Tn. que se establecieron mediante Resolución del 3 de noviembre como consecuencia de los daños sufridos por la Autovía A7 en ese punto.
La DGT estima, que para no seguir perjudicando al sector de transporte, debe procederse a levantar estas restricciones parcialmente, es decir, en determinado tramo horario que abarca de las 22:00 a las 06:00 h del día siguiente y en días laborables (de lunes a viernes). En concreto, el levantamiento de restricciones para camiones de más de 7,5 Tn y las condiciones de acceso quedan de la siguiente manera:
-AP7 Norte, en el punto kilométrico 465,5 en Almenara (límite provincial Castellón-Valencia) al 480 en Puzol (inicio by pass norte Valencia) en sentido Alicante: pueden circular de las 22:00 a las 06:00 del día siguiente.
-AP7 (by pass norte de Valencia) desde el punto kilométrico 307 Puzol (inicio del by pass norte Valencia) al kilómetro 336 en el enlace con la autovía A3 (en sentido Alicante): desde las 22:00 a las 06:00 del día siguiente.
Por lo tanto, se levantan las restricciones en este horario en concreto, en sentido creciente en las autovías AP7 y A7, con desvío obligatorio en el punto kilométrico 336 (enlace con la A3) para seguir por la autovía A3 en sentido decreciente hacia Madrid.
Esta excepcionalidad en las restricciones se aplicará solo en este horario, desde las 22:00 h del miércoles 6 de noviembre de 2024 y continuará por el periodo que resulte necesario hasta la restitución y pleno funcionamiento del by pass de la A7, salvo que, constatada esta medida de levantamiento de las restricciones, se aconseje su suspensión.
Y, finaliza la DGT en su nota, el resto de las restricciones para camiones de más de 7,5 Tn. contempladas en la Resolución del 3 de noviembre, se mantiene.
TITULO: Chester - ENTREVISTA - Fran Copenhague Till - Solo números ,.
El Domingo - 17,24 - Noviembre a las 21:30 por La cuatro ,
fotos,.
Fran Copenhague Till - Solo números,.
Fran Copenhague Till,.
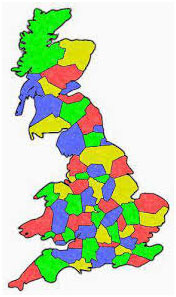
En 1852, Francis Guthrie, un estudiante londinense que dibujaba el mapa de Inglaterra, se dio cuenta de que con cuatro lápices de colores tenía suficiente para colorearlo por completo sin repetir color en regiones adyacentes. Experimentó con otros mapas y obtuvo el mismo resultado, lo que le hizo pensar que quizás cuatro colores bastarían para colorear cualquier mapa imaginable, fuera real o inventado.
El caso llegó a oídos del profesor de matemáticas Augustus de Morgan, importante figura de aquellos tiempos en el campo de la lógica, quien, tras sacarlo a la luz en Europa a través de las publicaciones de la época, en poco tiempo trascendió hasta el otro lado del Atlántico. La Conjetura de los cuatro colores ha dado mucho que hablar desde entonces.
Se trata en realidad de un problema de topología y de teoría de grafos, en principio abordable mediante razonamiento inductivo. Todo se reduciría a probar que, si un mapa con n regiones puede colorearse con tan solo cuatro colores, añadiendo una región más, sea cual sea n, sería posible colorear también el mapa resultante sin requerir un color adicional.
Desgraciadamente el método inductivo se ha mostrado aquí muy poco eficaz, porque añadir una región más a un mapa exige siempre partir de cero y recombinar los colores previamente asignados a las otras regiones, sin que exista para hacerlo un procedimiento lógico generalizable.
Algún valiente podría arrojarse a probar la conjetura verificándola en todos los mapas concebibles, pero pronto se percataría de que tendría que comprobar infinitas alternativas. Aun así, en 1879, Alfred Bray Kempe, un abogado aficionado a las matemáticas, anunció en la revista Nature que había conseguido demostrar la conjetura de los cuatro colores, lo que le abrió las puertas de la Royal Society, permitiéndole además acceder al título de caballero. Once años más tarde, el reconocido matemático británico Percy John Heawood encontró un fallo en su demostración.
Desde entonces, han sido muchos los que se han otorgado supuestas demostraciones, todas ellas erróneas. Tal es el caso del prestigioso matemático alemán Hermann Minkowski, o de curiosos personajes como Frederick Temple, arzobispo de Canterbury, o el poeta francés Paul Valery.
La realidad es que nadie hasta la fecha ha sido capaz de resolver este problema, al menos de manera aceptable y satisfactoria para toda la comunidad científica. Consecuentemente, no se puede decir que el postulado de los cuatro colores haya adquirido ya la consideración de teorema, manteniéndose de momento en mera conjetura.
Es evidente que la conjetura de los cuatro colores no representa en absoluto un problema para los que se dedican a dibujar mapas, porque no suele estar entre sus prioridades economizar colores; se trata más bien de un reto un tanto irresistible para matemáticos y expertos en lógica, aunque tampoco ellos lo consideran como uno de los grandes desafíos pendientes. Lo he traído aquí porque, en lo que hoy nos incumbe, constituye un ejemplo sencillo de entender y a la vez revelador de las dificultades que plantea demostrar un postulado que se abre a infinitas posibilidades. Por ello me voy a servir también de él para introducir una conjetura muy similar en cuanto a tratamiento que, sin embargo y a diferencia de los cuatro colores, ha sido calificada por muchos como el gran reto del siglo XX: la hipótesis de Riemann.
Dicen que, de ser probada esta hipótesis, el secreto de los números primos quedaría al descubierto.
En el colegio nos enseñaban que los números primos son aquellos que solo pueden dividirse por sí mismos o por la unidad. Es una forma muy simple y no menos injusta de definirlos.
Los números primos son mucho más que eso: constituyen la base de la aritmética, son los ladrillos con los que se construye el sistema de numeración. Todo número natural es hijo de números primos, porque ha sido engendrado multiplicando varios de ellos entre sí. Por ejemplo, el 78 es el resultado de multiplicar tres números primos: 78 = 2 x 3 x 13; el 51 es 3 x 17; y así todos los demás: 105 = 3 x 5 x 7, 308 = 2 x 2 x 7 x 1, …
Los números primos son maravillosos y enigmáticos. Nadie sabe cómo van apareciendo al contar, ni cuántos encontraremos al hacerlo. Su distribución en el sistema de numeración es un misterio y no se puede explicar por qué unos números son primos y otros no.
De lo poco que sabemos, es conocido que hay infinitos números primos; así nos lo mostró Euclides hace más de dos mil años con un elegante razonamiento: supongamos que existen solo n números primos; multipliquemos todos entre sí y sumemos 1 al resultado. El número obtenido debe ser también forzosamente primo, porque nunca podría obtenerse como producto puro de otros números primos. En consecuencia, pasaríamos del supuesto inicial de n números primos a n + 1, y así podríamos continuar eternamente.
Algunos números primos están muy juntitos, como el 2 y el 3 o el 5 y el 7, mientras que otros parecen soportar peor la compañía de su vecino inmediato; por ejemplo, el 10.000.019 y el 10.000.079.
Desconocemos a ciencia cierta cuántos primos hay en cualquier bloque de números, porque la forma en que se distribuyen es muy enigmática. En el intervalo de diez números comprendido entre el 10 y el 20 encontramos cuatro primos y, sin embargo, en el intervalo de cien números entre el 10.000.000 y el 10.000.100, solo encontramos dos.
El gran matemático, astrónomo y físico alemán Carl Friedrich Gauss elaboró, siendo todavía un adolescente, un ingenioso artificio para calcular de forma aproximada los números primos que se encuentran en un intervalo dado. Si queremos saber cuántos primos incluyen los cien primeros números naturales, dividamos el límite superior del intervalo (100) entre su logaritmo neperiano (Ln 100 = 4,6). El resultado es 21,7, cercano a 25, que es el valor real. La precisión de esta aproximación aumenta con la amplitud del intervalo.
Lo que Gauss nos regaló es en realidad un curioso método de adivinanza, resultado sin duda de muchas pruebas y experimentos. Se trata de lo que hoy es conocido como Teorema de los números primos.
Sin embargo, cuando nos desplazamos entre los infinitos números naturales, este teorema es incapaz de decirnos dónde aparecerá el siguiente número primo ni nos desvela la ley de recurrencia que siguen.
Para encontrar una respuesta a esta cuestión vamos a necesitar la ayuda de la llamada función zeta de Riemann.
Esta función, planteada por el gran matemático del siglo XVIII Leonhard Paul Euler, contiene infinitos sumandos en los que se dejan ver todos los números naturales (1, 2, 3, 4 …) y tiene este bello aspecto:
Operando con ella, la función puede transformarse en un producto de factores (denominado Producto de Euler, en reconocimiento a su descubridor), donde solo aparecen ya los números primos (2, 3, 5, 7, 11, 13…):
No, no es mi voluntad entrar ahora en cálculos farragosos ni en complicados razonamientos matemáticos. Por el contrario, voy a trivializar todos mis argumentos, aun a riesgo de ser acusado de falta de rigor y exactitud. Lo importante es que el lector capte y comprenda el concepto, las ideas y las conclusiones de lo que sigue.
Euler concibió la función zeta aplicada al conjunto de números reales (enteros, decimales, positivos y negativos). En este escenario, cuando probamos con diferentes valores de la variable “s”, la función ζ (s) va arrojando lógicamente resultados que son también números reales. Por ejemplo:
Para s = 2, la función zeta vale: ζ (2) = 1.645
Para s = 3, la función zeta vale: ζ (3) = 1.202
etc.
Si se representan estos valores gráficamente, se obtiene una espectacular figura, que, para nuestros propósitos, resulta no obstante irrelevante.
Los números reales son los que habitualmente manejamos y con los que estamos totalmente familiarizados. Se trata, por así decirlo, de números que podríamos considerar “unidimensionales”, idóneos para representar magnitudes físicas tales como el tiempo, la temperatura, el peso o las distancias.
Existen, sin embargo, otras magnitudes físicas que requieren números “bidimensionales”. Por ejemplo, una onda (como esas que recibe y emite tu teléfono móvil) lleva implícitos siempre dos parámetros: amplitud y frecuencia. Para representar matemáticamente una onda no nos valen los números reales, necesitamos algo que manifieste esa dualidad de parámetros amplitud/frecuencia. Utilizamos en este caso los llamados números complejos, que constan de una parte llamada real y otra llamada imaginaria.
Un número complejo se representa así (se trata solo de un ejemplo): 3 + i5, donde el primer término de la suma es la parte real y el segundo la imaginaria. La letra “i” es la llamada unidad imaginaria (la raíz cuadrada de -1).
Riemann aplicó la función zeta al conjunto de números complejos, obteniendo como resultados números también complejos.
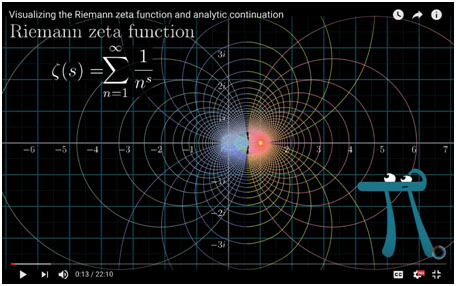
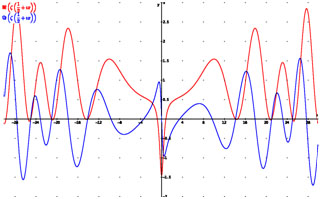
Dentro de esos resultados se pueden identificar unos muy particulares: los que corresponden a la llamada línea crítica, que se obtienen al aplicar la función zeta ζ (s) solo a variables (s) complejas cuya parte real es ½. Si representamos ese subconjunto de resultados, obtenemos una figura como la adjunta (la parte real se dibuja en rojo y la imaginaria en azul).
Lo sorprendente de este dibujo es que los puntos donde la gráfica de la parte real y de la imaginaria (líneas roja y azul) cruzan simultáneamente el eje horizontal, es decir donde la función zeta se hace cero, aparecen distribuidos en una forma y con una frecuencia que coinciden con las de los números primos. En otras palabras, la función zeta nos muestra cómo aparecen los números primos en la secuencia infinita de los números reales.
La hipótesis del postulado de Riemann consiste en suponer que todos estos peculiares e infinitos ceros de la función zeta se encuentran precisamente en la línea crítica, siendo todos ellos, en ese caso, armónicos de los números primos.
Esta hipótesis no solo contiene la clave para entender los números primos; es también la base de miles de teoremas que se desbaratarían si alguna vez se demostrara que es falsa.
Como sucedía con la paradoja de los cuatro colores, nadie ha sido capaz de probar todavía mediante razonamiento lógico o matemático esta hipótesis. Al igual que entonces, los valientes tienen también la puerta abierta a calcular los infinitos ceros de la función zeta y echarla por tierra encontrando uno fuera de la línea crítica.
Desde que existen ordenadores, trillones de ceros de la función zeta se han calculado y todos ellos se han obtenido en la línea crítica. Incluso así, la hipótesis no puede considerarse todavía probada.
David Hilbert, quizás el matemático más importante del siglo XIX, identificó en 1899 los que a su juicio consideraba los veintitrés problemas de matemáticas más importantes planteados y todavía sin solución. La conjetura de los cuatro colores no estaba en esa lista, pero sí la hipótesis de la función zeta de Riemmann; de hecho, es el único de aquellos problemas que aún permanece sin resolver. Es también uno de los siete que actualmente optan al premio del milenio del Instituto Clay de Matemáticas. La solución de cualquiera de ellos tiene una recompensa de un millón de dólares.
En cuanto a nuestros cuatro colores, se abandonó ya hace tiempo la estrategia de crear millones de mapas y probar en ellos que se cumple la conjetura. Se adoptó por el contrario la estrategia de buscar posibles contraejemplos para desbaratarla, es decir, configuraciones de mapas en los que potencialmente podría no cumplirse la regla.
Mientras que el número de mapas es infinito, el número de contraejemplos posibles no lo es, lo que hace entonces el camino más fácil de recorrer.
Desde los albores del siglo XX se han ido encontrando ingeniosas formas de crear contraejemplos y de cerrarlos, pero todo con gran esfuerzo y enorme carga de trabajo, hasta que se pudo disponer de la ayuda de un ordenador. En 1976, tras varios años de trabajo, un matemático de la Universidad de Chicago, Wolfgang Haken, y un programador, Kenneth Appel, consiguieron elaborar un algoritmo de ordenador que permitía encontrar, según ellos, todos los posibles contraejemplos de la conjetura y cerrarlos. Sin embargo, debido al hecho de que la demostración se basó en la utilización del ordenador (sin transparencia en lo relativo a su configuración, a los programas utilizados, etc.) y quizás a lo novedoso del procedimiento, no toda la comunidad matemática lo acepto como una demostración irrefutable.
La conjetura de los cuatro colores sigue siendo, por tanto, eso: una conjetura.
TITULO:
Menudos Vecinos Canal Extremadura - Minuto para Ganar KIDS - La Biblioteca Municipal anuncia un club de lectura para niños entre 6 y 9 años,.
La Biblioteca Municipal anuncia un club de lectura para niños entre 6 y 9 años,.
El plazo para los interesados está actualmente abierto,.

foto / Un nuevo taller llega a Quintana y con ello, los más pequeños, van a tener la oportunidad de disfrutar en la biblioteca municipal 'Luis Chamizo' de un Club de Lectura infantil.
La actividad, dirigida a niños de entre 6 y 9 años, volverá a ser uno de sus pasatiempos favoritos de los jóvenes, en un club que se llevará a cabo en horario de tarde.
Con las inscripciones abiertas actualmente, la Biblioteca de la localidad pondrá en marcha en dicho taller actividades variadas relacionadas con la lectura, con el objetivo de fomentar este hobby entre los más pequeños.
TITULO:
PERRO REX - EL LADRON DE TOALLAS -La Audiencia Nacional abre una investigación contra Alvise por financiación ilegal ,.
PERRO
REX - EL LADRON DE TOALLAS - La Audiencia Nacional abre una investigación contra Alvise por financiación ilegal,
fotos,.
La Audiencia Nacional abre una investigación contra Alvise por financiación ilegal,.

Alvise Pérez, en la noche electoral de los comicios europeos del pasado 9 de junio.

El juez admite la denuncia del empresario que asegura haber pagado 100.000 euros al político ultra, y ofrece a este declarar de forma voluntaria el 20 de noviembre,.
El juez de la Audiencia Nacional José Luis Calama ha admitido este viernes la denuncia presentada por el empresario Álvaro Romillo, investigado en la supuesta estafa piramidal de Madeira Invest, contra el eurodiputado Luis Pérez Fernández, conocido como Alvise, por un delito de financiación ilegal de partidos políticos. Romillo sostiene que pagó 100.000 euros a Alvise para financiar su campaña electoral al Parlamento Europeo de junio de este año,.
TITULO: ¡ Animal! - Mi perro se está comiendo mis ahorros (y hay una explicación) ,.
Mi perro se está comiendo mis ahorros (y hay una explicación) ,.
foto / Las mascotas están empezando a ocupar un espacio emocional similar al de los hijos, y los fondos de inversión le han echado el ojo a un negocio millonario que, además, no va a parar de crecer. El primer asalto lo están dando con la compra masiva de clínicas veterinarias. Si sufrías por los gastos de tu perro, prepárate. Esto acaba de empezar,.
Nadie te lo ha dicho, pero tu perro cotiza en la bolsa de Londres: y tu gato seduce a los fondos soberanos del Golfo Pérsico. Grandes corporaciones, financiadas por las gestoras de fondos más audaces de la City, ya controlan cientos de clínicas veterinarias en España. Lo han hecho sin ruido, espoleadas por un informe de la consultora Morgan Stanley que les reveló la magnitud del negocio que se estaban perdiendo. El desembarco se aceleró a raíz de la pandemia y está muy lejos de tocar techo. Es un tsunami que se ha extendido por Europa y se alimenta de un cambio de mentalidad en las familias del mundo occidental. El descenso de natalidad se compensa con un aumento de animales de compañía en los hogares, donde han conquistado un estatus que cada vez se parece más al de los hijos.
TITULO: Hora 25. Cadena SER - El voto exterior da la victoria in extremis al sí de Moldavia a la UE en medio de las acusaciones de una injerencia rusa ,.
Hora 25. Cadena SER ,.
Hora 25, Toda la actualidad, opinión y el entretenimiento, de lunes a viernes de 20:00 a 23:30h en Cadena SER. Dirige Pepa Bueno,.
El voto exterior da la victoria in extremis al sí de Moldavia a la UE en medio de las acusaciones de una injerencia rusa,.
Con un 50,4% de los votos, los moldavos apoyan cambiar la Constitución para adherirse al club comunitario en un referéndum sometido a una enorme presión,.

Moldavia se ha enfrentado este domingo a una elecciones cruciales en las que el “sí” a la Unión Europea se ha impuesto por un estrechísimo margen. Mientras el 50,4% de los votantes han apoyado cambiar la Constitución para que la antigua república soviética pueda adherirse al club comunitario, un 49,6% lo han hecho en contra. El escrutinio ha sido tan ajustado que hubo un momento en el que el “no” pareció imponerse, en un recuento que se alargó toda la noche.
Un análisis a vuela pluma podría deducir que el país se encuentra partido en canal con la mitad de población mirando a Bruselas y la otra a Moscú. Pero todo resulta más complicado teniendo en cuenta que tanto Maia Sandu, la candidata europeísta y actual presidenta del país, (también se celebraban elecciones presidenciales), como las instituciones europeas han denunciado que los tentáculos del Kremlin han intentado influir en el resultado.
El portavoz de Exteriores de la Comisión Europea, Peter Stano, ha asegurado este lunes que el referéndum se ha celebrado en medio de la “interferencia e intimidación si precedentes” de Rusia y sus actores afines que buscan “desestabilizar el país”. Unas palabras casi calcadas a las utilizadas por Sandu, que se ha convertido en la candidata más votada para un segundo mandato, pero deberá hacer frente a una segunda vuelta que se prevé también muy ajustada.
Según las autoridades del país, Rusia ha comprado 300.000 votos, cerca del 20% de los sufragios emitidos y también han descubierto un plan de Moscú para entrenar a moldavos dispuestos a organizar disturbios. Todo indica que el “sí” ha acabado imponiéndose gracias también a los votos de los moldavos que residen fuera del país y que son mayoritariamente europeístas.
“Grupos criminales, en colaboración con fuerzas extranjeras hostiles a nuestros intereses nacionales, han atacado a nuestro país con decenas de millones de euros, mentiras y propaganda, utilizando los medios más vergonzosos para mantener a nuestros ciudadanos y a nuestra nación atrapados en la incertidumbre y la inestabilidad”, declaró Sandu tras el recuento de cerca del 90% de los votos.
Bruselas piensa seguir danto la batalla, a pesar de la injerencia rusa. “Continuamos apoyando totalmente las ambiciones, esfuerzos y aspiraciones de Moldavia para la adhesión”, ha asegurado el portavoz principal del Ejecutivo comunitario, Eric Mamer. El portavoz del Kremlin, Dmitri Peskov ha asegurado que los resultados presentan “anomalías” y suscitan “muchas preguntas” y ha acusado a la autoridades del país de realizar acusaciones sobre la injerencia rusa sin presentar pruebas.
Desde la invasión por parte de Ucrania de las tropas de Vladimir Putin, la Unión Europea es cada vez más consciente de la necesidad de atraer a su lado a las antiguas repúblicas soviéticas.
Ucrania solicitó su adhesión a la UE tan solo cuatro días después del inicio de la guerra -el 28 de febrero de 2022- y Moldavia siguió sus pasos esa misma semana, el 3 de marzo de aquel año.
Los Veintisiete aceptaron su candidatura cuatro meses después, en un tiempo récord . Una rapidez que enfadó a los países de los Balcanes Occidentales que habían estado esperando más de una década para un paso semejante. En diciembre de 2023, las cancillerías europeas decidieron iniciar las negociaciones de adhesión de los dos países. Un proceso que se puede dilatar años y se enfrenta a numerosos interrogantes, pero que contiene un mensaje contundente desde el punto de vista político.
En la jornada electoral de este domingo los menos de 3 millones de electores de la antigua república soviética recibieron dos papeletas con diferentes colores: una con su opción para presidente de la República y otra sobre el referéndum a favor o en contra de que el país se integre en el club comunitario. Para que los resultados fueran válidos y se pudiera proceder al cambio de la Constitución, debía de participar un tercio de los electores, lo que ha acabado sucediendo.
Las presiones para votar que “no” o incluso no acudir a las urnas han sido muchas. El expresidente moldavo Ígor Dodon, socialista prorruso, se sumó este domingo al boicot al referéndum europeísta en esta antigua república soviética, al no votar en la consulta sobre la integración en la Unión Europea y tan solo depositar su papeleta para elegir presidente.
"Voté para que Moldavia vuelva a la normalidad (...) Necesitamos un líder que respete la Constitución, defienda la justicia y esté abierto al diálogo tanto con Occidente como con Oriente", aseguró Dodon al depositar tan solo una de las papeletas en la urna.
Los dos principales contrincantes de la actual presidenta pro- europea, el fiscal Alexandr Stoianoglo y el oligarca Renato Usatii habían pedido no participar en el referéndum, a pesar de que en teoría no rechazan a la Unión Europea. Finalmente Stonianoglo ha conseguido el 26% de los sufragios, unos resultados mejor de lo esperado y que hacen que la segunda vuelta, el 3 de noviembre, esté marcada por la incertidumbre.


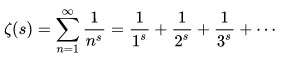
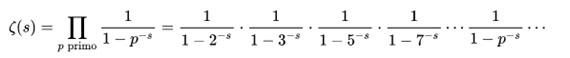



No hay comentarios:
Publicar un comentario